Elementos dos Triângulos:
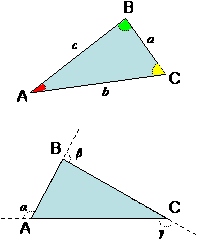
O triângulo é um polígono com três lados. Os três pontos não colineares são os vértices do triângulo: A, B e C.
As linhas que os unem são os lados do triângulo: [AB], [BC] e [AC].
Um vértice e o lado (oposto) que o não contém dizem-se opostos: o lado a é oposto a A. O lado b é oposto ao lado B e o lado c é oposto a C.Os ângulos internos do triângulo são os ângulos cujos vértices são os vértices do triângulo e os lados contêm os lados do triângulo. Assim temos três ângulos internos: ângulo ABC, ângulo ACB e ângulo BAC.
Há ainda a considerar os ângulos formados por cada lado e pelo prolongamento do outro lado, são os ângulos externos do triângulo: α, β e γ.
As linhas que os unem são os lados do triângulo: [AB], [BC] e [AC].
Um vértice e o lado (oposto) que o não contém dizem-se opostos: o lado a é oposto a A. O lado b é oposto ao lado B e o lado c é oposto a C.Os ângulos internos do triângulo são os ângulos cujos vértices são os vértices do triângulo e os lados contêm os lados do triângulo. Assim temos três ângulos internos: ângulo ABC, ângulo ACB e ângulo BAC.
Há ainda a considerar os ângulos formados por cada lado e pelo prolongamento do outro lado, são os ângulos externos do triângulo: α, β e γ.
Classificação dos triângulos:
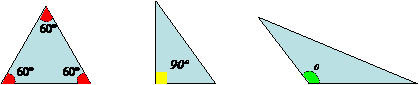
Os triângulos classificam-se:
Triângulo isósceles: Possui dois lados iguais e um diferente.
Triângulo escaleno: Possui todos os lados diferentes.
Triângulo retângulo: Possui um ângulo reto.
Triângulo obtusângulo: Possui um ângulo obtuso.
- Quanto ao lado:
Triângulo isósceles: Possui dois lados iguais e um diferente.
Triângulo escaleno: Possui todos os lados diferentes.
- Quanto aos ângulos:
Triângulo retângulo: Possui um ângulo reto.
Triângulo obtusângulo: Possui um ângulo obtuso.
Triângulos equilátero, isósceles e escaleno
Triângulos acutângulo, retângulo e obtusângulo
Pontos notáveis do triângulo:
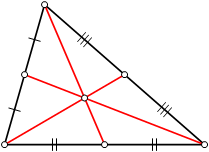
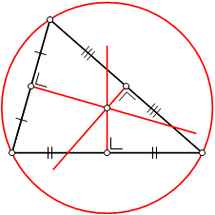
Se traçarmos o ponto médio de cada lado do triângulo (ponto que fica na metade do lado do triângulo), e traçarmos um segmento deste este ponto até o vértice oposto (mediana), estes se encontraram em um determinado ponto. Este ponto é chamado de Baricentro. O baricentro de um triângulo é o ponto pelo qual, se prendermos um barbante e suspendermos, o triângulo ficará em equilíbrio.
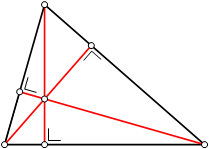
Todo lado de um triângulo possui uma altura. Se acharmos todas as alturas (reta perpendicular do vértice ao lado oposto), estas se encontraram em um ponto chamado de Ortocentro.
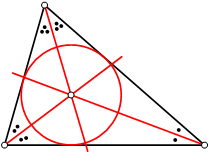
Por um vértice, é possível traçar uma bissetriz (segmento que divide o ângulo ao meio). Se fizermos todas as bissetrizes do triângulo, encontraremos um ponto que se chama Incentro. Pelo incentro é possível traçar uma circunferência inscrita no triângulo. Por ele também se percebe que ele tem a mesma distância (equidistante) de todos os lados do triângulo.
Quando obtemos as mediatrizes de um triângulo (retas perpendiculares a seus lados e que passam em seus respectivos pontos médios), encontramos um outro ponto chamado de circuncentro. O circuncentro é o centro da circunferência circunscrita de um triângulo.
Todo lado de um triângulo possui uma altura. Se acharmos todas as alturas (reta perpendicular do vértice ao lado oposto), estas se encontraram em um ponto chamado de Ortocentro.
Por um vértice, é possível traçar uma bissetriz (segmento que divide o ângulo ao meio). Se fizermos todas as bissetrizes do triângulo, encontraremos um ponto que se chama Incentro. Pelo incentro é possível traçar uma circunferência inscrita no triângulo. Por ele também se percebe que ele tem a mesma distância (equidistante) de todos os lados do triângulo.
Quando obtemos as mediatrizes de um triângulo (retas perpendiculares a seus lados e que passam em seus respectivos pontos médios), encontramos um outro ponto chamado de circuncentro. O circuncentro é o centro da circunferência circunscrita de um triângulo.
Baricentro
Incentro
|
Ortocentro
Circuncentro
|
Teorema de Pitágoras:
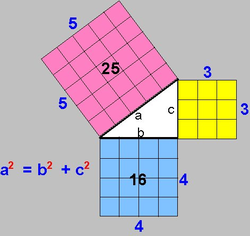
Teorema de Pitágoras
O Teorema de Pitágoras se refere a triângulos retângulos. Qualquer triângulo retângulo, como você sabe, têm um ângulo reto e dois ângulos agudos. Eles também possuem dois lados menores, chamados catetos, e um lada maior chamado hipotenusa.
Agora desenhe três quadrados,cujos lados medem 3, 4 e 5cm.
Vamos arrumar os quadrados que você desenhou. Note que o triangulo determinado pelos lados dos quadrados é um triângulo retângulo que tem catetos de medidas 3 e 4 e hipotenusa de medida 5. Por outro lado, você observou que a soma das áreas do quadrados menores dá a área do quadrado maior, ou seja, 9 + 16 = 25.
Isto é dito como a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Nós podemos usar o Teorema de Pitágoras em vários situações, então vamos escrever que em qualquer triângulo retângulo de hipotenusa a e catetos b e c, vale a relação:
a² = b² + c²
Para calcular isso precisamos seguir alguns passos:
1° - localizar a hipotenusa.
2° - substituir na fórmula.
*Isso é válido para triângulos retângulos. Veja o exemplo abaixo:
Num triângulo retângulo, os catetos medem 15cm e 8cm. Calcule a hipotenusa:
a² = 15² + 8²
a² = 225 + 64
a² = 289
a = √289
a = 17
Agora desenhe três quadrados,cujos lados medem 3, 4 e 5cm.
Vamos arrumar os quadrados que você desenhou. Note que o triangulo determinado pelos lados dos quadrados é um triângulo retângulo que tem catetos de medidas 3 e 4 e hipotenusa de medida 5. Por outro lado, você observou que a soma das áreas do quadrados menores dá a área do quadrado maior, ou seja, 9 + 16 = 25.
Isto é dito como a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Nós podemos usar o Teorema de Pitágoras em vários situações, então vamos escrever que em qualquer triângulo retângulo de hipotenusa a e catetos b e c, vale a relação:
a² = b² + c²
Para calcular isso precisamos seguir alguns passos:
1° - localizar a hipotenusa.
2° - substituir na fórmula.
*Isso é válido para triângulos retângulos. Veja o exemplo abaixo:
Num triângulo retângulo, os catetos medem 15cm e 8cm. Calcule a hipotenusa:
a² = 15² + 8²
a² = 225 + 64
a² = 289
a = √289
a = 17
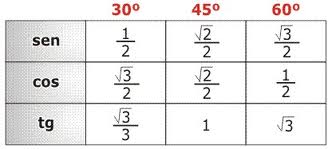
Razões trigonométricas:
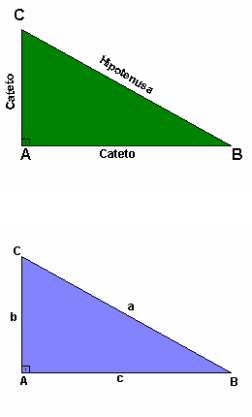
- Catetos e Hipotenusa:
Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes de catetos.
Observe a figura ao lado:
Hipotenusa: BC
Catetos: Ab e AC
- Seno, cosseno e tangente:
Considere um triângulo retângulo BAC:
Tomando por base os elementos desse triângulo, podemos definir as seguintes razões trigonométricas:
Abaixo segue as fórmulas para calcular o seno, o cosseno e a tangente:
Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes de catetos.
Observe a figura ao lado:
Hipotenusa: BC
Catetos: Ab e AC
- Seno, cosseno e tangente:
Considere um triângulo retângulo BAC:
Tomando por base os elementos desse triângulo, podemos definir as seguintes razões trigonométricas:
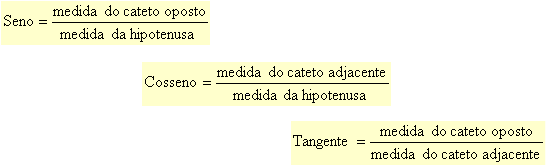
- Seno de um ângulo agudo é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa.
- Cosseno de um ângulo agudo é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa.
- Tangente de um ângulo agudo é a razão entre a medida do cateto oposto e a medida do cateto adjacente a esse ângulo.
Abaixo segue as fórmulas para calcular o seno, o cosseno e a tangente:
- Observações:
- A tangente de um ângulo agudo pode ser definida como a razão entre seno deste ângulo e o seu cosseno.
- A tangente de um ângulo agudo é um número real positivo.
- O seno e o cosseno de um ângulo agudo são sempre números reais positivos menores que 1, pois qualquer cateto é sempre menor que a hipotenusa.
Principais razões trigonométricas
