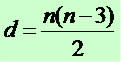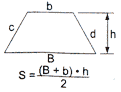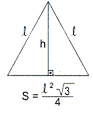Polígonos:
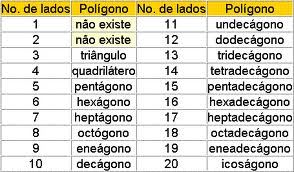
Polígonos são figuras fechadas formadas por segmentos de reta, sendo caracterizados pelos seguintes elementos: ângulos, vértices, diagonais e lados. De acordo com o número de lados a figura pode ser classificada como:
Classificação dos Polígonos
Polígonos convexos e côncavos:
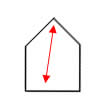
Polígono Convexo: se unir quaisquer dos seus pontos, o segmento de reta obtido está sempre contido no polígono.
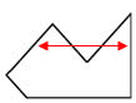
Polígono Côncavo oi não-convexo: se existem, pelo menos, dois pontos que unidos, formam um segmento de reta que não se encontra contido no polígono, este será côncavo.
Polígono Côncavo oi não-convexo: se existem, pelo menos, dois pontos que unidos, formam um segmento de reta que não se encontra contido no polígono, este será côncavo.
Polígono convexo
|
Polígono côncavo
|
Polígonos regulares e irregulares:
Todo polígono regular possui os lados e os ângulos com medidas iguais.
Um polígono irregular é aquele que não possui os ângulos com medidas iguais e os lados não possuem o mesmo tamanho.
Um polígono irregular é aquele que não possui os ângulos com medidas iguais e os lados não possuem o mesmo tamanho.
Polígonos Regulares
|
Polígonos Irregulares
|
Diagonais de um polígono:
Diagonal de um polígono é o segmento de reta que liga um vértice ao outro, passando pelo interior da figura. O número de diagonais de um polígono depende do número de lados (n) e pode ser calculado pela expressão:
Ângulos internos e externos:
Em um polígono, quanto maior o número de lados, maior a medida dos ângulos internos.
Considerando as diagonais traçadas por apenas um dos vértices de um polígono, é possível perceber que elas formam triângulos. Conforme aumentamos os lados de um polígono, a quantidade de triângulos aumenta, veja:
Em um quadrilátero conseguimos formar 2 triângulos.
Considerando que em cada triângulo a soma dos ângulos internos iguais é 180°, então a soma dos ângulos internos de qualquer quadrilátero será 2 * 180° = 360°.
Em um polígono de cinco lados (pentágono) formamos 3 triângulos.
Dessa forma, temos que a soma dos ângulos internos de um pentágono é 180° * 3 = 540°
Em um polígono de seis lados (hexágono) formamos 4 triângulos.
Portanto, a soma dos ângulos internos é dada por 4 * 180° = 720°.
Percebemos que a diferença do número de triângulos formados e o número de lados dos polígonos é sempre 2, então concluímos que:
n = 3 ; Si = (3 – 2) * 180° = 1 * 180° = 180°
n = 4 ; Si = (4 – 2) * 180° = 2 * 180° = 360°
n = 5 ; Si = (5 – 2) * 180° = 3 * 180° = 540°
n = 6 ; Si = (6 – 2) * 180° = 4 * 180° = 720°
n = n ; Si = (n – 2) * 180°
Portanto, a soma dos ângulos internos de qualquer polígono será calculada através da expressão: Si = (n – 2) * 180°
Caso queira calcular o valor de cada ângulo interno, basta dividir a soma dos ângulos internos pelo número de lados do polígono. Mas vale lembrar que esta fórmula abaixo só deve ser utilizada em polígonos regulares, pois estes possuem os ângulos internos iguais.
ai = Si / n
- Soma dos ângulos externos de um polígono regular:
A soma dos ângulos externos de qualquer polígono convexo, independentemente da quantidade de lados, é igual a 360°.
Obs.: A soma de um ângulo interno com o seu respectivo externo é igual a 180°, isto é, eles são suplementares.
Considerando as diagonais traçadas por apenas um dos vértices de um polígono, é possível perceber que elas formam triângulos. Conforme aumentamos os lados de um polígono, a quantidade de triângulos aumenta, veja:
Em um quadrilátero conseguimos formar 2 triângulos.
Considerando que em cada triângulo a soma dos ângulos internos iguais é 180°, então a soma dos ângulos internos de qualquer quadrilátero será 2 * 180° = 360°.
Em um polígono de cinco lados (pentágono) formamos 3 triângulos.
Dessa forma, temos que a soma dos ângulos internos de um pentágono é 180° * 3 = 540°
Em um polígono de seis lados (hexágono) formamos 4 triângulos.
Portanto, a soma dos ângulos internos é dada por 4 * 180° = 720°.
Percebemos que a diferença do número de triângulos formados e o número de lados dos polígonos é sempre 2, então concluímos que:
n = 3 ; Si = (3 – 2) * 180° = 1 * 180° = 180°
n = 4 ; Si = (4 – 2) * 180° = 2 * 180° = 360°
n = 5 ; Si = (5 – 2) * 180° = 3 * 180° = 540°
n = 6 ; Si = (6 – 2) * 180° = 4 * 180° = 720°
n = n ; Si = (n – 2) * 180°
Portanto, a soma dos ângulos internos de qualquer polígono será calculada através da expressão: Si = (n – 2) * 180°
Caso queira calcular o valor de cada ângulo interno, basta dividir a soma dos ângulos internos pelo número de lados do polígono. Mas vale lembrar que esta fórmula abaixo só deve ser utilizada em polígonos regulares, pois estes possuem os ângulos internos iguais.
ai = Si / n
- Soma dos ângulos externos de um polígono regular:
A soma dos ângulos externos de qualquer polígono convexo, independentemente da quantidade de lados, é igual a 360°.
Obs.: A soma de um ângulo interno com o seu respectivo externo é igual a 180°, isto é, eles são suplementares.
Cálculo de Perímetro e Área:
O perímetro é o comprimento da linha ou do contorno de uma determinada figura (polígono). Ou ainda, é a soma das medidas dos lados de um polígono.
Área é a medida de uma superfície.
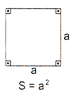
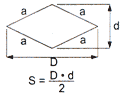
Abaixo temos as fórmulas do cálculo de área de alguns polígonos:
Área é a medida de uma superfície.
Abaixo temos as fórmulas do cálculo de área de alguns polígonos:
Área do Quadrado
Área do Retângulo
|
Área do Paralelogramo
Área do Triângulo
|
Área do Losango
Área do Trapézio
|
Área do Triângulo Equilátero
|