Função:
O estudo do produto cartesiano serviu de base para aprendermos sobre as relações. Estas agora são o alicerce para o estudo das funções, por isto, para que você assimile melhor este conceito, é importante que você revise os tópicos sobre produto cartesiano e relações.
As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica.
Veja a imagem abaixo:
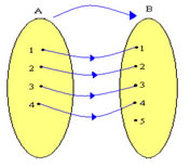
Observe que todos os elementos do conjunto A possuem uma flecha em direção a um único elemento do conjunto B.
Em outras palavras, não há no conjunto A qualquer elemento que não esteja associado a um elemento do conjunto B e os elementos de A estão associados a apenas um elemento de B.
Por possuir tal propriedade, dizemos que esta relação é uma função f de A em B representada por:
f: A -> B
As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica.
Veja a imagem abaixo:
Observe que todos os elementos do conjunto A possuem uma flecha em direção a um único elemento do conjunto B.
Em outras palavras, não há no conjunto A qualquer elemento que não esteja associado a um elemento do conjunto B e os elementos de A estão associados a apenas um elemento de B.
Por possuir tal propriedade, dizemos que esta relação é uma função f de A em B representada por:
f: A -> B
- Domínio da Função:
Ao conjunto A damos o nome de domínio da função.
O domínio é o conjunto de partida. Ele composto de todos os elementos do conjunto de partida.
Neste nosso exemplo o domínio da função f é representado por D(f) = { 1, 2, 3, 4 }, ou seja, o domínio desta função contém todos os elementos do conjunto A.
Como supracitado, para que tenhamos uma função, todos os elementos do domínio devem estar associados a um e somente um dos elementos de B.
- Contradomínio da Função:
Ao conjunto B damos o nome de contradomínio da função.
O contradomínio é o conjunto de chegada. Ele é composto de todos os elementos do conjunto de chegada.
Em nosso exemplo o contradomínio da função f é representado por CD(f) = { 1, 2, 3, 4, 5 }, isto é, o contradomínio desta função contém todos os elementos do conjunto B.
Segundo o conceito de função não é necessário que todos os elementos de B estejam relacionados aos elementos do domínio. Note que no conjunto B o elemento 5 não recebe nenhuma flecha, isto é, não está relacionado a qualquer elemento de A.
Uma outra coisa que deve ser observada é que em uma função os elementos do contradomínio podem receber mais de uma flechada, se associando, portanto, a mais de um elemento do domínio.
- Imagem da Função:
A imagem da função dependendo do caso é o próprio contradomínio, ou então é um subconjunto seu.
Os elementos do conjunto imagem são todos os elementos do contradomínio que estão associados a algum elemento do domínio. No exemplo que estamos utilizando o conjunto imagem é representado por Im(f) = { 1, 2, 3, 4 }, pois 1, 2, 4 e 4 são todos os elementos do CD(f) que estão associados a algum elemento do D(f).
Em resumo para a função de exemplo temos:
Domínio da Função: D(f) = { 1, 2, 3, 4 }
Contradomínio da Função: CD(f) = { 1, 2, 3, 4, 5 }
Conjunto Imagem da Função: Im(f) = { 1, 2, 3, 4 }
Nesta função exemplo o conjunto imagem é um subconjunto do contradomínio, pois o elemento 5 de B não está contido no conjunto imagem, por não estar associado a nenhum elemento do domínio.
Ao conjunto A damos o nome de domínio da função.
O domínio é o conjunto de partida. Ele composto de todos os elementos do conjunto de partida.
Neste nosso exemplo o domínio da função f é representado por D(f) = { 1, 2, 3, 4 }, ou seja, o domínio desta função contém todos os elementos do conjunto A.
Como supracitado, para que tenhamos uma função, todos os elementos do domínio devem estar associados a um e somente um dos elementos de B.
- Contradomínio da Função:
Ao conjunto B damos o nome de contradomínio da função.
O contradomínio é o conjunto de chegada. Ele é composto de todos os elementos do conjunto de chegada.
Em nosso exemplo o contradomínio da função f é representado por CD(f) = { 1, 2, 3, 4, 5 }, isto é, o contradomínio desta função contém todos os elementos do conjunto B.
Segundo o conceito de função não é necessário que todos os elementos de B estejam relacionados aos elementos do domínio. Note que no conjunto B o elemento 5 não recebe nenhuma flecha, isto é, não está relacionado a qualquer elemento de A.
Uma outra coisa que deve ser observada é que em uma função os elementos do contradomínio podem receber mais de uma flechada, se associando, portanto, a mais de um elemento do domínio.
- Imagem da Função:
A imagem da função dependendo do caso é o próprio contradomínio, ou então é um subconjunto seu.
Os elementos do conjunto imagem são todos os elementos do contradomínio que estão associados a algum elemento do domínio. No exemplo que estamos utilizando o conjunto imagem é representado por Im(f) = { 1, 2, 3, 4 }, pois 1, 2, 4 e 4 são todos os elementos do CD(f) que estão associados a algum elemento do D(f).
Em resumo para a função de exemplo temos:
Domínio da Função: D(f) = { 1, 2, 3, 4 }
Contradomínio da Função: CD(f) = { 1, 2, 3, 4, 5 }
Conjunto Imagem da Função: Im(f) = { 1, 2, 3, 4 }
Nesta função exemplo o conjunto imagem é um subconjunto do contradomínio, pois o elemento 5 de B não está contido no conjunto imagem, por não estar associado a nenhum elemento do domínio.
Função do 1º grau:
O estudo das funções é importante, uma vez que elas podem ser aplicadas em diferentes circunstâncias: nas engenharias, no cálculo estatístico de animais em extinção, etc.
O significado de função é intrínseco à matemática, permanecendo o mesmo para qualquer tipo de função, seja ela do 1° ou do 2° grau, ou uma função exponencial ou logarítmica. Portanto, a função é utilizada para relacionar valores numéricos de uma determinada expressão algébrica de acordo com cada valor que a variável x assume.
Sendo assim, a função do 1° grau relacionará os valores numéricos obtidos de expressões algébricas do tipo (ax + b), constituindo, assim, a função f(x) = ax + b.
Note que para definir a função do 1° grau, basta haver uma expressão algébrica do 1° grau. Como dito anteriormente, o objetivo da função é relacionar para cada valor de x um valor para o f(x). Vejamos um exemplo para a função f(x)= x – 2.
x = 1, temos que f(1) = 1 – 2 = –1
x = 4, temos que f(4) = 4 – 2 = 2
Note que os valores numéricos mudam conforme o valor de x é alterado, sendo assim obtemos diversos pares ordenados, constituídos da seguinte maneira: (x, f(x)). Veja que para cada coordenada x, iremos obter uma coordenada f(x). Isso auxilia na construção de gráficos das funções.
O significado de função é intrínseco à matemática, permanecendo o mesmo para qualquer tipo de função, seja ela do 1° ou do 2° grau, ou uma função exponencial ou logarítmica. Portanto, a função é utilizada para relacionar valores numéricos de uma determinada expressão algébrica de acordo com cada valor que a variável x assume.
Sendo assim, a função do 1° grau relacionará os valores numéricos obtidos de expressões algébricas do tipo (ax + b), constituindo, assim, a função f(x) = ax + b.
Note que para definir a função do 1° grau, basta haver uma expressão algébrica do 1° grau. Como dito anteriormente, o objetivo da função é relacionar para cada valor de x um valor para o f(x). Vejamos um exemplo para a função f(x)= x – 2.
x = 1, temos que f(1) = 1 – 2 = –1
x = 4, temos que f(4) = 4 – 2 = 2
Note que os valores numéricos mudam conforme o valor de x é alterado, sendo assim obtemos diversos pares ordenados, constituídos da seguinte maneira: (x, f(x)). Veja que para cada coordenada x, iremos obter uma coordenada f(x). Isso auxilia na construção de gráficos das funções.
Propriedades de uma função:
- Função sobrejetora:
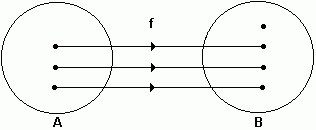
É aquela cujo conjunto imagem é igual ao contradomínio, ou seja, Im=B.
- Função injetora:
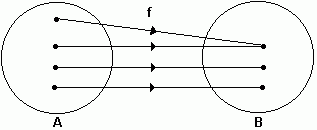
Uma função y = f(x) é injetora quando elementos distintos do seu domínio, possuem imagens distintas, ou seja, dois elementos não podem ter a mesma imagem.
- Função bijetora:
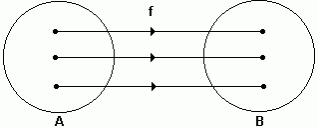
Uma função é dita bijetora, quando ela é ao mesmo tempo injetora e sobrejetora .
É aquela cujo conjunto imagem é igual ao contradomínio, ou seja, Im=B.
- Função injetora:
Uma função y = f(x) é injetora quando elementos distintos do seu domínio, possuem imagens distintas, ou seja, dois elementos não podem ter a mesma imagem.
- Função bijetora:
Uma função é dita bijetora, quando ela é ao mesmo tempo injetora e sobrejetora .