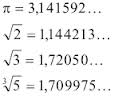Conjuntos Numéricos:
Número é um objeto da matemática usado para descrever quantidade, ordem ou medida. O conceito de número provavelmente foi um dos primeiros conceitos matemáticos assimilados pela humanidade no processo de contagem.
- História dos números:
O conceito de número está associada com a capacidade de contar e comparar qual de dois conjuntos de entidades semelhantes é o maior. As primeiras sociedades humanas encontraram dificuldades em determinar qual de dois conjuntos era "maior" do que outro, ou para saber com precisão quantos itens formavam uma coleção de coisas. Esses problemas podem ser resolvidos com uma simples contagem. A maioria das culturas têm sistemas de contagem que atingem pelo menos centenas, algumas outras mais simples têm condições apenas de enumerar os números 1, 2 e 3 e usam o termo "muitos" para quantidades maiores.
A contagem comecou a ser feita usando objetos físicos (tais como pilhas de pedras) e marcas como aquelas encontradas em ossos. Os sistemas de numeração na maioria dos idiomas mostram que a contagem esta associada com os dedos das mãos (sistema decimal).
Os registros de números com a utilização de símbolos escritos é associado ao o surgimento de sociedades mais complexas aonde passaram a ser necessários registros contábeis e burocráticos, registros fiscais e de propriedade.
- História dos números:
O conceito de número está associada com a capacidade de contar e comparar qual de dois conjuntos de entidades semelhantes é o maior. As primeiras sociedades humanas encontraram dificuldades em determinar qual de dois conjuntos era "maior" do que outro, ou para saber com precisão quantos itens formavam uma coleção de coisas. Esses problemas podem ser resolvidos com uma simples contagem. A maioria das culturas têm sistemas de contagem que atingem pelo menos centenas, algumas outras mais simples têm condições apenas de enumerar os números 1, 2 e 3 e usam o termo "muitos" para quantidades maiores.
A contagem comecou a ser feita usando objetos físicos (tais como pilhas de pedras) e marcas como aquelas encontradas em ossos. Os sistemas de numeração na maioria dos idiomas mostram que a contagem esta associada com os dedos das mãos (sistema decimal).
Os registros de números com a utilização de símbolos escritos é associado ao o surgimento de sociedades mais complexas aonde passaram a ser necessários registros contábeis e burocráticos, registros fiscais e de propriedade.
Números Naturais:
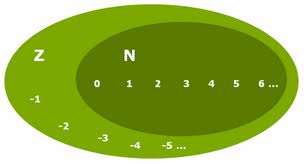
Um número natural é um número inteiro não-negativo (0, 1, 2, 3,...). O número natural também é definido como um número inteiro positivo, aonde o zero não é considerado como um número natural. Quando o símbolo dos números naturais (N) vier seguido de um asterisco (*) é retirado o 0 (zero).
- N = {0,1,2,3,4,5,6,7,8,9,10, …}
- N* = {1,2,3,4,5,6,7,8,9,10, …}
Números Inteiros:
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:
- Inteiros não negativos:
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:
São todos os números inteiros que não são positivos. É representado por Z-:
Z- = {…, -5, -4, -3, -2, -1, 0}
- Inteiros não negativos e não nulos:
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
São representados pela letra Z:
- Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4, …}
- Inteiros não negativos:
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:
- Z+ = {0,1,2,3,4,5,6, …}
São todos os números inteiros que não são positivos. É representado por Z-:
Z- = {…, -5, -4, -3, -2, -1, 0}
- Inteiros não negativos e não nulos:
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
- Z*+ = {1, 2, 3, 4, 5, 6, 7, …}
- Z*+ = N*
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
- Z*- = {… -4, -3, -2, -1}
Conjunto dos Números Inteiros
Números Racionais:
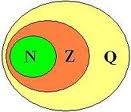
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por exemplo: 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como “12,050505…”, são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.
- Números Fracionários:
Fração é um modo de expressar uma quantidade a partir de um valor que é dividido por um determinado número de partes iguais entre si. Número fracionário expressa esta condição. A palavra vem do latim fractus e significa "partido", "quebrado" (do verbo frangere: "quebrar"). estes números estão incluídos nos números racionais.
Os racionais são representados pela letra Q.
- Números Fracionários:
Fração é um modo de expressar uma quantidade a partir de um valor que é dividido por um determinado número de partes iguais entre si. Número fracionário expressa esta condição. A palavra vem do latim fractus e significa "partido", "quebrado" (do verbo frangere: "quebrar"). estes números estão incluídos nos números racionais.
Conjunto dos Números Racionais
Números Irracionais:
É formado pelos números decimais infinitos não-periódicos. Um bom exemplo de número irracional é o número PI (resultado da divisão do perímetro de uma circunferência pelo seu diâmetro), que vale 3,14159265 …. Atualmente, supercomputadores já conseguiram calcular bilhões de casas decimais para o PI.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 …)
A primeira descoberta de um número irracional é geralmente atribuída a Hipaso de Metaponto, um seguidor de Pitágoras.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 …)
A primeira descoberta de um número irracional é geralmente atribuída a Hipaso de Metaponto, um seguidor de Pitágoras.
Conjunto dos Números Irracionais
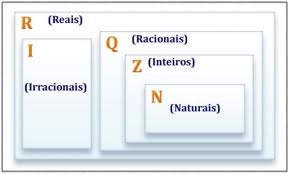
Números Reais:
É formado por todos os conjuntos citados anteriormente (união do conjunto dos racionais com os irracionais).
Representado pela letra R.
Representado pela letra R.
Conjunto dos Números Reais
