Porcentagem:
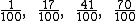
As frações (ou razões) que possuem denominadores (o número de baixo da fração) iguais a 100, são conhecidas por razões centesimais e podem ser representadas pelo símbolo "%".
O símbolo "%" é lido como "por cento". "5%" lê-se "5 por cento". "25%" lê-se "25 por cento".
O símbolo "%" significa centésimos, assim "5%" é uma outra forma de se escrever 0,05, ou por exemplo.
Veja as razões ao lado:Podemos representá-las na sua forma decimal por:
0,01; 0,17; 0,41; 0,70.
E também na sua forma de porcentagens por:
1%; 17%; 41%; 70%.
- Como calcular um valor percentual de um número?
Agora que temos uma visão geral do que é porcentagem, como calcular quanto é 25% de 200?
Multiplique 25 por 200 e divida por 100:
(25 . 200):100=50
Se você achar mais fácil, você pode simplesmente multiplicar 25% na sua forma decimal, que é 0,25 por 200:
0,25 . 200=50
Assim temos:
Analisando os itens de 1 a 4, podemos também perceber que quando o percentual é menor 100%, o número resultante será menor que o número original. Nos itens 6 e 7 percebemos que o resultado é maior que o número original. Isto ocorre porque o percentual é maior que 100%.
Nos itens 2 e 3 observamos que 15% de 180 é igual a 18% de 150. a% de b é igual a b% de a. Isto é devido à propriedade comutativa da multiplicação que diz que a . b = b . a.
O símbolo "%" é lido como "por cento". "5%" lê-se "5 por cento". "25%" lê-se "25 por cento".
O símbolo "%" significa centésimos, assim "5%" é uma outra forma de se escrever 0,05, ou por exemplo.
Veja as razões ao lado:Podemos representá-las na sua forma decimal por:
0,01; 0,17; 0,41; 0,70.
E também na sua forma de porcentagens por:
1%; 17%; 41%; 70%.
- Como calcular um valor percentual de um número?
Agora que temos uma visão geral do que é porcentagem, como calcular quanto é 25% de 200?
Multiplique 25 por 200 e divida por 100:
(25 . 200):100=50
Se você achar mais fácil, você pode simplesmente multiplicar 25% na sua forma decimal, que é 0,25 por 200:
0,25 . 200=50
Assim temos:
- 4% de 32 = 0,04 . 32 = 1,28
- 15% de 180 = 0,15 . 180 = 27
- 18% de 150 = 0,18 . 150 = 27
- 35% de 126 = 0,35 . 126 = 44,1
- 100% de 715 = 1,00 . 715 = 715
- 115% de 60 = 1,15 . 60 = 69
- 200% de 48 = 2,00 . 48 = 96
Analisando os itens de 1 a 4, podemos também perceber que quando o percentual é menor 100%, o número resultante será menor que o número original. Nos itens 6 e 7 percebemos que o resultado é maior que o número original. Isto ocorre porque o percentual é maior que 100%.
Nos itens 2 e 3 observamos que 15% de 180 é igual a 18% de 150. a% de b é igual a b% de a. Isto é devido à propriedade comutativa da multiplicação que diz que a . b = b . a.
Raízes:
- Raiz quadrada:
Sabemos que 3² = 9. O número 3 pode ser escrito √9 e lê raiz quadrada de 9. Dizemos que 3 = √9. O sinal √, chamado radical é a modificação da letra r. O número 9 é chamado radicando. Como √9 é 3, temos que -√9 = -3.
Quando escrevemos , por exemplo, √49, estamos nos referindo ao número não negativo que elevado ao quadrado dá 49, que no caso é 7.
(-2)² = 4. No entanto, não escrevemos √4 = -2, pois √4 é reservado para denotar o número 2.
Dizer 3² = 9 é o mesmo que dizer √9 = 3. Indicamos isso escrevendo 3² = 9 ⇔ √9 = 3. Lembramos que o símbolo ⇔ lê-se se, "e somente se" ou "é equivalente a". Veja as principais raízes quadradas:
a) √4 = 2
b) √9 = 3
c) √16 = 4
d) √25 = 5
e) √36 = 6
f) √49 = 7
g) √64 = 8
h) √81 = 9
- Raiz cúbica:
2³ = 8. Escrevemos, então, 2 = ³√8 e lê-se 2 é igual à raiz cúbica de 8. O número 3 é colocado no radical é chamado índice (no caso da raiz quadrada, o índice é 2, mas usualmente não é colocado.Colocar o 2, porém, não é erro. Assim, √4 = ²√4 = 2.).
Como ³√8 = 2, temos que -³√8 = -2.
Escrever ³√27 é, portanto, referir-se ao número que elevado ao cubo dá 27, que no caso é 3. Assim ³√27 = 3.
(-2)³ = -8. Escrevemos, então, -2 = ³√-8.
Observar que -2 é também -³√8. Logo ³√-8 = -³√8.
Sabemos que 3² = 9. O número 3 pode ser escrito √9 e lê raiz quadrada de 9. Dizemos que 3 = √9. O sinal √, chamado radical é a modificação da letra r. O número 9 é chamado radicando. Como √9 é 3, temos que -√9 = -3.
Quando escrevemos , por exemplo, √49, estamos nos referindo ao número não negativo que elevado ao quadrado dá 49, que no caso é 7.
(-2)² = 4. No entanto, não escrevemos √4 = -2, pois √4 é reservado para denotar o número 2.
Dizer 3² = 9 é o mesmo que dizer √9 = 3. Indicamos isso escrevendo 3² = 9 ⇔ √9 = 3. Lembramos que o símbolo ⇔ lê-se se, "e somente se" ou "é equivalente a". Veja as principais raízes quadradas:
a) √4 = 2
b) √9 = 3
c) √16 = 4
d) √25 = 5
e) √36 = 6
f) √49 = 7
g) √64 = 8
h) √81 = 9
- Raiz cúbica:
2³ = 8. Escrevemos, então, 2 = ³√8 e lê-se 2 é igual à raiz cúbica de 8. O número 3 é colocado no radical é chamado índice (no caso da raiz quadrada, o índice é 2, mas usualmente não é colocado.Colocar o 2, porém, não é erro. Assim, √4 = ²√4 = 2.).
Como ³√8 = 2, temos que -³√8 = -2.
Escrever ³√27 é, portanto, referir-se ao número que elevado ao cubo dá 27, que no caso é 3. Assim ³√27 = 3.
(-2)³ = -8. Escrevemos, então, -2 = ³√-8.
Observar que -2 é também -³√8. Logo ³√-8 = -³√8.
Fatorial:
Ao produto dos números naturais começando em n e decrescendo até 1 denominamos de fatorial de n e representamos por n!.
Segundo tal definição, o fatorial de 5 é representado por 5! e lê-se 5 fatorial.
5! é igual a 5 . 4 . 3 . 2 . 1 que é igual a 120, assim como 4! é igual a 4 . 3 . 2 . 1 que é igual a 24, como 3! é igual a 3 . 2 . 1 que é igual a 6 e que 2! é igual a 2 . 1 que é igual a 2.
Por definição tanto 0!, quanto 1! são iguais a 1.
- Escrevendo um fatorial a partir de um outro fatorial menor:
Vimos que 5! é equivalente a 5 . 4 . 3 . 2 . 1, mas note que também podemos escrevê-lo de outras formas, em função de fatoriais menores, tais como 4!, 3! e 2!:
5! = 5 . 4!
5! = 5 . 4 . 3!
5! = 5 . 4 . 3 . 2!
Para um fatorial genérico temos:
n! = n . (n - 1)! = n . (n - 1) . (n - 2)! = n . (n - 1) . (n - 2) . (n - 3) . ... . 1!
Observe atentamente os exemplos seguintes:
(n + 3)! = (n + 3) . (n + 2)!
(n + 3)! = (n + 3) . (n + 2) . (n + 1)!
(n + 1)! = (n + 1) . n!
Vamos atribuir a n o valor numérico 6, para termos uma visão mais clara destas sentenças:
9! = 9 . 8!
9! = 9 . 8 . 7!
7! = 7 . 6!
Estes conceitos são utilizados em muitos dos problemas envolvendo fatoriais.
Segundo tal definição, o fatorial de 5 é representado por 5! e lê-se 5 fatorial.
5! é igual a 5 . 4 . 3 . 2 . 1 que é igual a 120, assim como 4! é igual a 4 . 3 . 2 . 1 que é igual a 24, como 3! é igual a 3 . 2 . 1 que é igual a 6 e que 2! é igual a 2 . 1 que é igual a 2.
Por definição tanto 0!, quanto 1! são iguais a 1.
- Escrevendo um fatorial a partir de um outro fatorial menor:
Vimos que 5! é equivalente a 5 . 4 . 3 . 2 . 1, mas note que também podemos escrevê-lo de outras formas, em função de fatoriais menores, tais como 4!, 3! e 2!:
5! = 5 . 4!
5! = 5 . 4 . 3!
5! = 5 . 4 . 3 . 2!
Para um fatorial genérico temos:
n! = n . (n - 1)! = n . (n - 1) . (n - 2)! = n . (n - 1) . (n - 2) . (n - 3) . ... . 1!
Observe atentamente os exemplos seguintes:
(n + 3)! = (n + 3) . (n + 2)!
(n + 3)! = (n + 3) . (n + 2) . (n + 1)!
(n + 1)! = (n + 1) . n!
Vamos atribuir a n o valor numérico 6, para termos uma visão mais clara destas sentenças:
9! = 9 . 8!
9! = 9 . 8 . 7!
7! = 7 . 6!
Estes conceitos são utilizados em muitos dos problemas envolvendo fatoriais.
