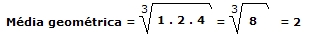Números e frações decimais:
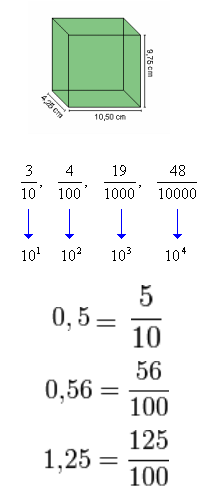
A figura ao lado nos mostra um paralelepípedo com suas principais dimensões em centímetros.
Essas dimensões são apresentadas sob a forma de notação decimal, que corresponde a uma outra forma de representação dos números racionais fracionários.
A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète.O uso dos números decimais é bem superior ao dos números fracionários. Observe que nos computadores e nas máquinas calculadoras utilizamos unicamente a forma decimal.
Observe as frações ao lado:
Estas frações denominam-se frações decimais,ou seja, todas as frações que apresentam potências de 10 no denominador.
- Numeração Decimal:
O francês Viète (1540 - 1603) desenvolveu um método para escrever as frações decimais; no lugar de frações, Viète escreveria números com vírgula. Esse método, modernizado, é utilizado até hoje.
Observe os números ao lado representados por frações decimais e por números decimais:
Os números 0,1; 0,01; 0,001; 11,7, por exemplo, são números decimais. Nessa representação, verificamos que a vírgula separa a parte inteira da parte decimal. No caso do 1,25; a parte inteira é o 1 e a parte decimal é o 25.
Essas dimensões são apresentadas sob a forma de notação decimal, que corresponde a uma outra forma de representação dos números racionais fracionários.
A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète.O uso dos números decimais é bem superior ao dos números fracionários. Observe que nos computadores e nas máquinas calculadoras utilizamos unicamente a forma decimal.
Observe as frações ao lado:
Estas frações denominam-se frações decimais,ou seja, todas as frações que apresentam potências de 10 no denominador.
- Numeração Decimal:
O francês Viète (1540 - 1603) desenvolveu um método para escrever as frações decimais; no lugar de frações, Viète escreveria números com vírgula. Esse método, modernizado, é utilizado até hoje.
Observe os números ao lado representados por frações decimais e por números decimais:
Os números 0,1; 0,01; 0,001; 11,7, por exemplo, são números decimais. Nessa representação, verificamos que a vírgula separa a parte inteira da parte decimal. No caso do 1,25; a parte inteira é o 1 e a parte decimal é o 25.
Divisibilidade:
- Números Primos:
Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo.
Exemplos:
- Mínimo Múltiplo Comum:
Como 24 é divisível por 3 dizemos que 24 é múltiplo de 3. 24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...
Observações importantes:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.
Dois números naturais sempre têm divisores comuns. Por exemplo: os divisores comuns de 12 e 18 são 1,2,3 e 6. Dentre eles, 6 é o maior. Então chamamos o 6 de máximo divisor comum de 12 e 18 e indicamos m.d.c.(12,18) = 6.
Os números 35 e 24 são números primos entre si, pois mdc (35,24) = 1.
Os números 35 e 21 não são números primos entre si, pois mdc (35,21) = 7.
Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo.
Exemplos:
- 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo.
- 17 tem apenas os divisores 1 e 17, portanto 17 é um número primo.
- 10 tem os divisores 1, 2, 5 e 10, portanto 10 não é um número primo.
- 1 não é um número primo, porque ele tem apenas um divisor que é ele mesmo.
- 2 é o único número primo que é par.
- Mínimo Múltiplo Comum:
Como 24 é divisível por 3 dizemos que 24 é múltiplo de 3. 24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.
- Se um número é divisível por outro, diferente de zero, então dizemos que ele é múltiplo desse outro.
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...
Observações importantes:
- Um número tem infinitos múltiplos
- Zero é múltiplo de qualquer número natural
- MÍNIMO MÚLTIPLO COMUM (M.M.C.)
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.
- O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum desses números. Usamos a abreviação m.m.c.
Dois números naturais sempre têm divisores comuns. Por exemplo: os divisores comuns de 12 e 18 são 1,2,3 e 6. Dentre eles, 6 é o maior. Então chamamos o 6 de máximo divisor comum de 12 e 18 e indicamos m.d.c.(12,18) = 6.
- O maior divisor comum de dois ou mais números é chamado de máximo divisor comum desses números. Usamos a abreviação m.d.c.
- mdc (6,12) = 6
- mdc (12,20) = 4
- mdc (20,24) = 4
- mdc (12,20,24) = 4
- mdc (6,12,15) = 3
- Dois ou mais números são primos entre si quando o máximo divisor comum desses números é 1.
Os números 35 e 24 são números primos entre si, pois mdc (35,24) = 1.
Os números 35 e 21 não são números primos entre si, pois mdc (35,21) = 7.
Critérios de Divisibilidade:
Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade.
Exemplos:
1) 5040 é divisível por 2, pois termina em 0.
2) 237 não é divisível por 2, pois não é um número par.
Exemplo:
234 é divisível por 3, pois a soma de seus algarismos é igual a 2+3+4=9, e como 9 é divisível por 3, então 234 é divisível por 3.
Exemplos:
1) 55 é divisível por 5, pois termina em 5.
2) 90 é divisível por 5, pois termina em 0.
3) 87 não é divisível por 5, pois não termina em 0 nem em 5.
Exemplos:
1) 312 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 6).
2) 5214 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 12).
3) 716 não é divisível por 6, (é divisível por 2, mas não é divisível por 3).
4) 3405 não é divisível por 6 (é divisível por 3, mas não é divisível por 2).
Exemplo:
2871 é divisível por 9, pois a soma de seus algarismos é igual a 2+8+7+1=18, e como 18 é divisível por 9, então 2871 é divisível por 9.
Exemplos:
1) 4150 é divisível por 10, pois termina em 0.
2) 2106 não é divisível por 10, pois não termina em 0.
- Divisibilidade por 2:
Exemplos:
1) 5040 é divisível por 2, pois termina em 0.
2) 237 não é divisível por 2, pois não é um número par.
- Divisibilidade por 3:
Exemplo:
234 é divisível por 3, pois a soma de seus algarismos é igual a 2+3+4=9, e como 9 é divisível por 3, então 234 é divisível por 3.
- Divisibilidade por 5:
Exemplos:
1) 55 é divisível por 5, pois termina em 5.
2) 90 é divisível por 5, pois termina em 0.
3) 87 não é divisível por 5, pois não termina em 0 nem em 5.
- Divisibilidade por 6:
Exemplos:
1) 312 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 6).
2) 5214 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 12).
3) 716 não é divisível por 6, (é divisível por 2, mas não é divisível por 3).
4) 3405 não é divisível por 6 (é divisível por 3, mas não é divisível por 2).
- Divisibilidade por 9:
Exemplo:
2871 é divisível por 9, pois a soma de seus algarismos é igual a 2+8+7+1=18, e como 18 é divisível por 9, então 2871 é divisível por 9.
- Divisibilidade por 10:
Exemplos:
1) 4150 é divisível por 10, pois termina em 0.
2) 2106 não é divisível por 10, pois não termina em 0.
Médias:
- Média aritmética simples:
A média aritmética simples também é conhecida apenas por média. Ela está tão presente em nosso dia-a-dia que qualquer pessoa entende seu significado e a utiliza com frequência. A média de um conjunto de valores numéricos é calculada somando-se todos estes valores e dividindo-se o resultado pelo número de elementos somados, que é igual ao número de elementos do conjunto, ou seja, a média de n números é sua soma dividida por n. Por exemplo, a média entre 5, 10 e 6 será: 5 + 6 + 10 = 21/3 = 7.
- Média geométrica:
Entre n valores, é a raiz de índice n do produto desses valores. Veja no exemplo, a média geométrica entre 1, 2 e 4:
A média aritmética simples também é conhecida apenas por média. Ela está tão presente em nosso dia-a-dia que qualquer pessoa entende seu significado e a utiliza com frequência. A média de um conjunto de valores numéricos é calculada somando-se todos estes valores e dividindo-se o resultado pelo número de elementos somados, que é igual ao número de elementos do conjunto, ou seja, a média de n números é sua soma dividida por n. Por exemplo, a média entre 5, 10 e 6 será: 5 + 6 + 10 = 21/3 = 7.
- Média geométrica:
Entre n valores, é a raiz de índice n do produto desses valores. Veja no exemplo, a média geométrica entre 1, 2 e 4:
- Média aritmética ponderada:
A média ponderada é calculada através do somatório das multiplicações entre valores e pesos divididos pelo somatório dos pesos. Exemplo: Na escola de Gabriel, a média anual de cada matéria é calculada de acordo com os princípios da média ponderada. Considerando que o peso das notas esteja relacionado ao bimestre em questão, determine a média anual de Gabriel sabendo que as notas em Matemática foram iguais a:
1º Bimestre: 7,0
2º Bimestre: 6,0
3º Bimestre: 8,0
4º Bimestre: 7,5
A média ponderada é calculada através do somatório das multiplicações entre valores e pesos divididos pelo somatório dos pesos. Exemplo: Na escola de Gabriel, a média anual de cada matéria é calculada de acordo com os princípios da média ponderada. Considerando que o peso das notas esteja relacionado ao bimestre em questão, determine a média anual de Gabriel sabendo que as notas em Matemática foram iguais a:
1º Bimestre: 7,0
2º Bimestre: 6,0
3º Bimestre: 8,0
4º Bimestre: 7,5