Circunferência

Conceito de Circunferências e Círculos:

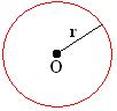
A circunferência pode ser considerada uma linha curva fechada, onde a distância entre a extremidade e qualquer ponto da mesma possui medida igual.

Qualquer segmento determinado pelo centro e por um ponto da circunferência é igual ao raio.

O segmento que une dois pontos distintos quaisquer de uma circunferência é chamado de corda. 

Diâmetro é sempre a corda maior (passa pelo centro) e sua medida é igual a duas vezes a medida do raio. 

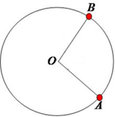
Observe a circunferência da figura 2. Os dois pontos A e B dividem a circunferência em duas partes chamadas arcos. O arco maior é o BA, e o arco menor é o AB. Notem que o arco é medido no sentido anti-horário. 

Círculo é a região da circunferência com sua região interna.

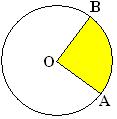
Setor circular é a parte do círculo limitada por dois raios.

Raio

Arcos

Setor circular

---

Posições relativas entre circunferência e reta:

Num plano, uma reta e uma circunferência podem ter em comum dois pontos distintos, um único ponto ou nenhum ponto. Vamos estudar esses três casos:

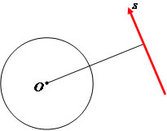
• Reta externa à circunferência:

A reta s é externa à circunferência de centro O e raio R, então podemos propor a seguinte situação: a distância do centro da circunferência à reta s é maior que o raio da circunferência. 
D > R

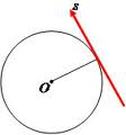
• Reta tangente à circunferência:

A reta s é tangente à circunferência de centro O e raio R, isto é, a reta s possui um ponto em comum com a circunferência, por isso podemos dizer que a distância entre centro O até a reta s possui a mesma medida. 
D = R 

• Reta secante à circunferência:

A reta s é secante à circunferência de raio R e centro O, a reta intersecta a circunferência em dois pontos. Nesse caso constatamos que a medida do raio da circunferência é maior que a medida da reta secante. 
D < R 

Reta externa

Reta tangente

Reta secante

---

Relações Métricas:

A circunferência possui algumas importantes relações métricas envolvendo segmentos internos, secantes e tangentes. Através dessas relações obtemos as medidas procuradas. 

- Relação entre as cordas:
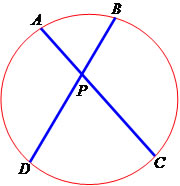
O cruzamento de duas cordas na circunferência gera segmentos proporcionais, e a multiplicação entre as medidas das duas partes de uma corda é igual à multiplicação das medidas das duas partes da outra corda. Observe:

Relação entre as cordas

PA.PC = PB.PD

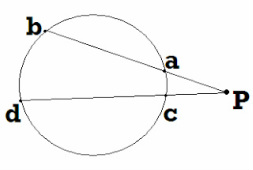
- Relação entre secantes:
Em qualquer circunferência, quando traçamos dois segmentos secantes, partindo de um mesmo ponto, a multiplicação da medida de um deles pela medida de sua parte externa é igual à multiplicação da medida do outro segmento pela medida de sua parte externa. Observe:

Relação entre secantes

PA.PB = PC.PD

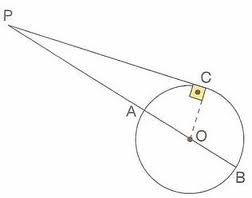
- Relação entre secante e tangente:
Nesse caso, o quadrado da medida do segmento tangente é igual à multiplicação da medida do segmento secante pela medida de sua parte externa.

Relação entre secante e tangente

PC² = PA.PB